Mineral Accretion Technology Power Analysis
research 09 Aug 2023Overview
My goal with this first mineral accretion technology (MAT) experiment is to understand 1) if the technology enhances growth rates, and 2) if certain morphologies (branching v. massive) preferentially respond to MAT. The results from this preliminary experiment will inform subsequent experiments, which will first identify the optimal electrochemical conditions and then incorporate ocean acidification and genotype effects. Since this is a preliminary experiment to robustly assess the efficacy of MAT, I want to have adequate statistical power to setup success for future experiments. In other words, if MAT doesn’t work, why bother with the more arduous experiments. Thus, the goal of this exercise is to estimate the number of fragments per species needed to maintain appropriate statistical power.
The idea behind the morphologies responding differently to MAT is the distance of the primary growth axis from the steel cathode. In branching species, such as A. cervicornis, the fast-growing apical tip is farthest from the cathode, where carbonates are being converted during electrolysis. Conversely, massive coral species with their compact morphology places the actively growing polyps more proximate to the site of altered water chemistry. Thus, an initial hypothesis is that massive corals will have a greater percentage increase in growth rates than branching corals.
I want to incorporate the two most commonly used species in Florida coral restoration, Acropora cervicornis (ACER) and Pseudodiploria strigosa (PSTR) OR Montastrea cavernosa (MCAV). There will be two treatment groups (electrified/non-electrified), and an n=2 for each treatment. All parameters (presence of platinum anode, steel cathode as the coral base structure, wires connecting everything, peristaltic pump in the center of the aquarium, etc.) will be equal, except that the wires will not be connected to the power supply in the non-electrified aquaria. To account for genet-specific growth rates, I will collect four ramets from each genet and divide equally among the four experimental aquaria. Thus each genet will be represented twice within treatment and once within each aquaria.
Table 1. Count of putative genets in the Caribbean and Florida restoration networks, aggregrated from Coral Sample Registry database. Florida data is a subset of Caribbean data.
| Species | Caribbean | Florida | % Florida |
|---|---|---|---|
| Acropora cervicornis | 420 | 327 | 77.9 |
| Montastraea cavernosa | 264 | 228 | 86.4 |
| Pseudodiploria strigosa | 254 | 225 | 88.6 |
| Diploria labyrinthiformis | 189 | 187 | 98.9 |
| Colpophyllia natans | 185 | 171 | 92.4 |
| Meandrina meandrites | 192 | 171 | 89.1 |
| Orbicella faveolata | 313 | 170 | 54.3 |
| Eusmilia fastigiata | 165 | 164 | 99.4 |
| Mycetophyllia aliciae | 161 | 161 | 100.0 |
| Acropora palmata | 504 | 156 | 31.0 |
| Dichocoenia stokesii | 141 | 139 | 98.6 |
| Mussa angulosa | 88 | 88 | 100.0 |
| Pseudodiploria clivosa | 62 | 62 | 100.0 |
| Mycetophyllia lamarckiana | 58 | 58 | 100.0 |
| Orbicella annularis | 82 | 57 | 69.5 |
| Agaricia lamarcki | 26 | 26 | 100.0 |
| Millepora complanata | 16 | 16 | 100.0 |
| Siderastrea siderea | 17 | 13 | 76.5 |
| Mycetophyllia ferox | 11 | 11 | 100.0 |
| Stephanocoenia intersepta | 10 | 10 | 100.0 |
| Porites astreoides | 7 | 7 | 100.0 |
| Porites porites | 12 | 5 | 41.7 |
| Acropora prolifera | 4 | 4 | 100.0 |
| Dendrogyra cylindrus | 49 | 4 | 8.2 |
| Solenastrea bournoni | 3 | 3 | 100.0 |
| Oculina diffusa | 2 | 2 | 100.0 |
| Orbicella franksi | 43 | 2 | 4.7 |
| Agaricia agaricites | 1 | NA | 0.0 |
| Favia fragum | 3 | NA | 0.0 |
| Isophyllia sinuosa | 1 | NA | 0.0 |
| Meandrina jacksoni | 1 | NA | 0.0 |
| Porites divaricata | 1 | NA | 0.0 |
| Siderastrea radians | 10 | NA | 0.0 |
Within the wider Caribbean region, Acropora palmata (504) is the dominant species in coral restoration due to its preponderance in Puerto Rico restoration efforts led by Sea Ventures/NOAA (322 records of the 504 putative genets). A. palmata is followed by A. cervicornis (420), Orbicella faveolata (313), M. cavernosa (264), and P. strigosa (254). When we focus solely on Florida coral restoration efforts, A. cervicornis (327) is the most cultivated species as expected followed by M. cavernosa (228) and P. strigosa (225). Thus, using A. cervicornis as the branching species and M. cavernosa or P. strigosa as the massive species in this preliminary experiment would be appropriate.
Estimating MAT Mean Effect
The following is a table of published and unpublished data I have aggregated. While I have encountered many more references, their results section are incomplete (missing averages and/or standard deviations of control and treatment groups) and were unable to be cast into this analysis.
Table 2. Summary of literature review effect sizes
| author | doi | growth | effect size | cohens d |
|---|---|---|---|---|
| Huang | 10.1080/14634988.2020.1768766 | 31 % | 0.54000 | 1.3000 |
| Borell | 10.1007/s00338-009-0564-y | 64 % | 0.82450 | 3.0000 |
| Kihara | 10.3755/galaxea.15.323 | 8 % | 0.25400 | 0.5250 |
| Sabater & Yap | 10.1016/S0022-0981(02)00051-5 | -5 % | 0.53000 | 1.2500 |
| Samidon | 10.3389/fmars.2022.917360 | 17 % | 0.40325 | 0.8895 |
| Damayanti | NA | 298 % | 0.93350 | 5.2093 |
| Natasasmita | 10.15406/jamb.2016.04.00086 | 20 % | 0.82500 | 2.9150 |
If we trust this data (which I don’t; hence why I’m running this preliminary experiment instead of jumping in), then we can expect a median percentage increase in coral growth of 20 %.
Calculating Group Sizes
I collected growth rates from the Perry coral growth database, which aggregates calcification data for their ReefBudget surveys. While these data are likely not predictive of what we will observe in the laboratory with the buoyant weight methodology, the relative differences in growth rates among species provides a framework for us to build this statistical power model.
Next, I estimated power-sample size curves with pooled standard deviations (SD) varying from 0.05 - 0.25 $g \text{ } cm^{-2} \text{ } yr^{-1}$ with 0.05 increments and percent increases in growth rates relative to control from 5-50% in 5% increments. Effect sizes at each combination of pooled SD and percent increase were estimated.
Our 2-factor anova will have the following form: aov(G ~ treatment * species). There will be 2 levels to treatment and 2 levels to species. The significance of an interactive effect (treatment:species) suggests that at least one of the species responded differently to the MAT compared to the other two.
Table 3. Estimated mean growth rates per species per % increase in growth rate conferred by MAT. % increase are arbitrary numbers ranging from 5-50% increased growth rates
| species | Control | 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACER | 7.2720 | 7.63560 | 7.99920 | 8.36280 | 8.72640 | 9.09000 | 9.45360 | 9.81720 | 10.18080 | 10.54440 | 10.9080 |
| MCAV | 0.6198 | 0.65079 | 0.68178 | 0.71277 | 0.74376 | 0.77475 | 0.80574 | 0.83673 | 0.86772 | 0.89871 | 0.9297 |
| PSTR | 0.5888 | 0.61824 | 0.64768 | 0.67712 | 0.70656 | 0.73600 | 0.76544 | 0.79488 | 0.82432 | 0.85376 | 0.8832 |
Figure 1. Group-size power curves for estimated % increase in growth rates. Vertical line denotes 80% power.
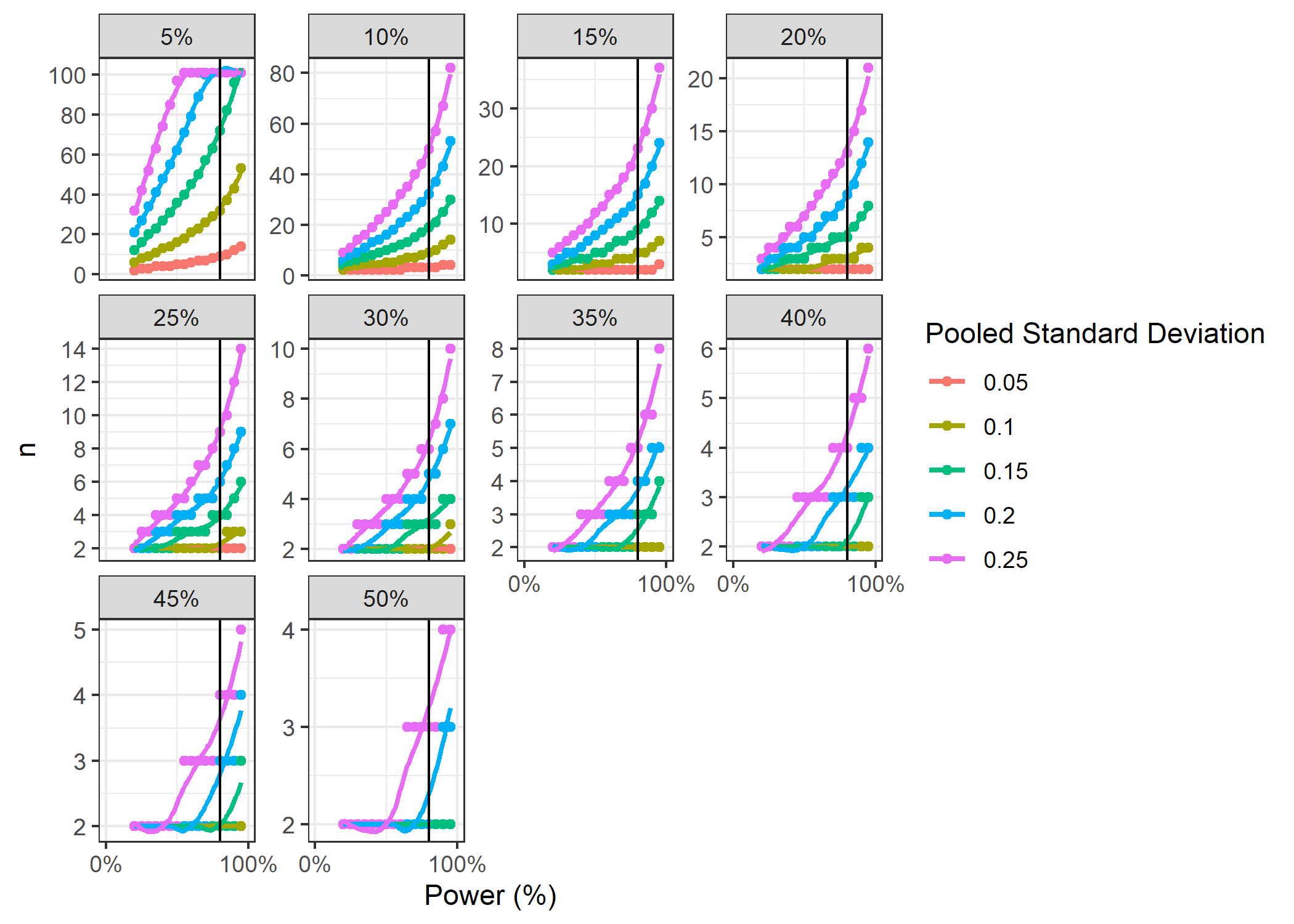
From these power-sample size curves, we can see that we need at least 14 fragments per treatment group to have 80% power and detect a 20% increase in MAT if the pooled SD is less than or equal to 0.25 $g \text{ } cm^{-2} \text{ } yr^{-1}$. With that same treatment size and goal of at least 80% power, we would be able to detect a 15% increase in growth rates if the pooled SD was less than or equal to 0.15 $g \text{ } cm^{-2} \text{ } yr^{-1}$, a 10% increase in growth rates if the pooled SD was less than or equal to 0.10 $g \text{ } cm^{-2} \text{ } yr^{-1}$, or a 5% increase in growth rates if the pooled SD was less than or equal to 0.05. When the observed increase in growth rates due to MAT is greater than or equal to 25%, there is greater than 95% power when the standard deviation is 0.25 $g \text{ } cm^{-2} \text{ } yr^{-1}$ or less.
If the observed growth rate is a modest 10% and the pooled SD is 0.25 $g \text{ } cm^{-2} \text{ } yr^{-1}$, then we would only have 30% power with an n=14. We would need 50 fragments per group to detect a 10% increase with the same pooled SD, which is unfeasible. However, if MAT only increases growth rates by 10%, it would not be able to overcome the decreases in growth rates expected by ocean acidification.
Since we have two aquariums per treatment, we can divide the required sample size evenly and have seven fragments per species per aquarium. When we run the final analysis, we will create two models. One model will be a two way anova as described above. The second model will incorporate the aquarium as a random effect, which will be compared against the fixed effects model. Ideally, there is no statistical advantage gained from the mixed effects model (as judged by AIC) since the two aquaria will have equal treatment conditions and should thus exhibit the same growth patterns. Nevertheless, incorporating this mixed effects model will likely improve the statistical power compared to a normal fixed-effects ANOVA if the standard deviation is greater than what was estimated above.
Mixed Effects Power
Calculating power and effect sizes on mixed effects models is a bit more difficult. The best way to do it is to simulate data multiple times and take the averages. The Superpower package makes this relatively easy. For each of the simulations, I set the number of fragments per treatment per aquarium at 7 fragments and identified the maximum pooled SD to maintian 80% power. This is equivalent to the 80% power gained from having 14 fragments with a 20% increase in MAT with a pooled SD less than or equal to 0.25 $g \text{ } cm^{-2} \text{ } yr^{-1}$.
When there is 20% increase in growth rates, the pooled SD can increase to 0.75. This demonstrates the added power, or the ability to have more variation within treatment/species groups and maintain statistical power, when employing a mixed-effects model.
Electrical Considerations
With an n=7 per treatment per aquarium, that gives us n=7 x 2 species + 3 blanks/aquarium = 17 cathodes per aquarium. The blanks are to acount for abiotic precipiation of abiotic electrodeposits, which are hypothesized to be uniform (given current density and cathodes are identical) within a treatment. At a surface area of 21 $cm^2$, that will be a total cathode surface area of 357 $cm^2$ or 0.0357 $m^2$. Since I would like to test current densities between 0.5-5.0 A/m2, I will need to supply each aquarium between 14 - 140 mA, well within the range of our capabilities. For this experiment, I will only employ one current density to test whether MAT increases growth rate. If it indeed does, a second preliminary expeirmnet will investigate the optimal current density.